煮杯热茶

算法介绍

这里记录学习《算法图解》的笔记。

二分法查找

顾名思义，它是一种算法，从一个有序的列表中查找目标元素，使用从中间位置开始向目标元素靠近。例如，目标元素在 1-100 的数字中，你从 50 开始猜测，如果小了，就取 50-100 的中间位置继续猜测，则反之。 一般而言，对于包含 n 个元素的列表，用二分查找最多需要 步，而简单查找最多需要 n 步。

大 O 表示法

随着数据量的不断增加，处理数据的时间是如何变化的，缓慢速度增加、平均速度增加、快速增加等等。（操作数也多，说明用时越长。）

选择排序

  1. 计算机内存犹如一大堆抽屉。
  2. 需要存储多个元素时，可使用数组或链表。
  3. 数组的元素都在一起。
  4. 链表的元素是分开的，其中每个元素都存储了下一个元素的地址。
  5. 数组的读取速度很快。
  6. 链表的插入和删除速度很快。
  7. 在同一个数组中，所有元素的类型都必须相同（都为 int、double 等）。

递归

  1. 递归指的是调用自己的函数。
  2. 每个递归函数都有两个条件：基线条件和递归条件。
  3. 栈有两种操作：压入和弹出。
  4. 所有函数调用都进入调用栈。
  5. 调用栈可能很长，这将占用大量的内存。

提示：编写涉及数组的递归函数时，基线条件通常是数组为空或只包含一个元素。陷入困境时， 请检查基线条件是不是这样的。

快速排序

  1. 快速排序将问题逐步分解。使用快速排序处理列表时，基线条件很可能是空数组或只包含一个元 素的数组。
  2. 实现快速排序时，请随机地选择用作基准值的元素。快速排序的平均运行时间为 O()。
  3. 大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因所在。
  4. 比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O() 的速度比 O(n) 快得多。

散列表

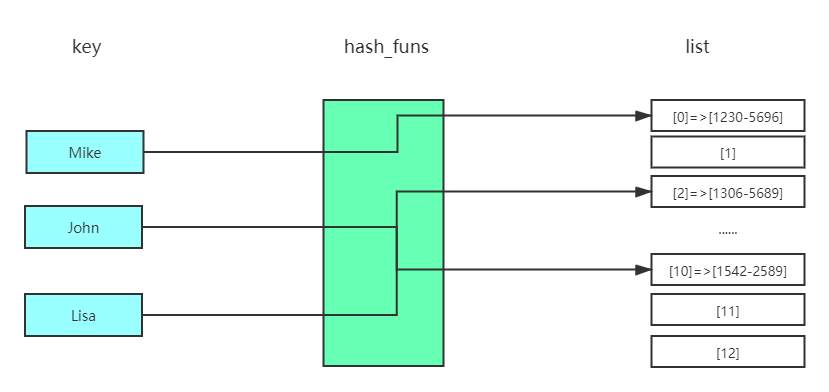
散列表即是哈希（hash）表。 散列/哈希函数：将输入映射到数字（键映射到值）。

哈希表

通过链表解决哈希冲突

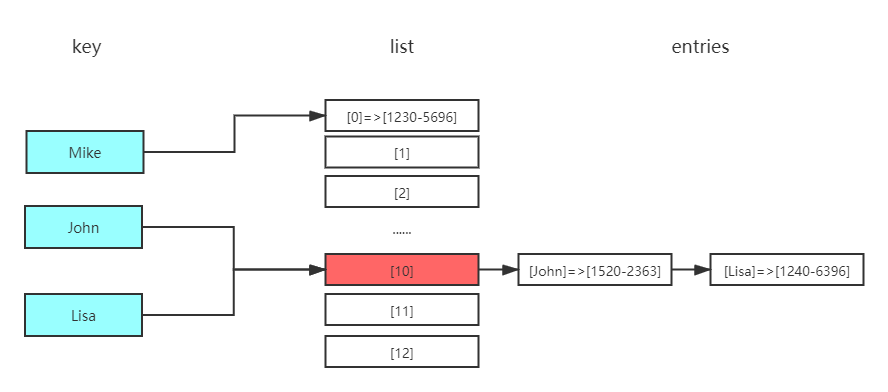
哈希表冲突

  1. 你可以结合散列函数和数组来创建散列表。
  2. 冲突很糟糕，你应使用可以最大限度减少冲突的散列函数。
  3. 散列表的查找、插入和删除速度都非常快。
  4. 散列表适合用于模拟映射关系。
  5. 一旦填装因子超过 0.7，就该调整散列表的长度。
  6. 散列表可用于缓存数据（例如，在 Web 服务器上）。
  7. 散列表非常适合用于防止重复。

广度优先搜索

  1. 广度优先搜索指出是否有从A到B的路径。
  2. 如果有，广度优先搜索将找出最短路径。
  3. 面临类似于寻找最短路径的问题时，可尝试使用图来建立模型，再使用广度优先搜索来 解决问题。
  4. 有向图中的边为箭头，箭头的方向指定了关系的方向，例如，rama→adit表示rama欠adit钱。
  5. 无向图中的边不带箭头，其中的关系是双向的，例如，ross - rachel表示“ross与rachel约 会，而rachel也与ross约会”。
  6. 队列是先进先出（FIFO）的。
  7. 栈是后进先出（LIFO）的。
  8. 你需要按加入顺序检查搜索列表中的人，否则找到的就不是最短路径，因此搜索列表必 须是队列。
  9. 对于检查过的人，务必不要再去检查，否则可能导致无限循环。

狄克斯特拉算法

步骤：

  1. 找出最便宜的节点，即可在最短时间内前往的节点。
  2. 对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。
  3. 重复这个过程，直到对图中的每个节点都这样做了。
  4. 计算最终路径。
  • 广度优先搜索用于在非加权图中查找最短路径。
  • 狄克斯特拉算法用于在加权图中查找最短路径。
  • 仅当权重为正时狄克斯特拉算法才管用。
  • 如果图中包含负权边，请使用贝尔曼福德算法。

贪婪算法

  • 贪婪算法寻找局部最优解，企图以这种方式获得全局最优解。
  • 对于 NP 完全问题，还没有找到快速解决方案。
  • 面临 NP 完全问题时，最佳的做法是使用近似算法。
  • 贪婪算法易于实现、运行速度快，是不错的近似算法。

动态规划

  • 需要在给定约束条件下优化某种指标时，动态规划很有用。
  • 问题可分解为离散子问题时，可使用动态规划来解决。
  • 每种动态规划解决方案都涉及网格。
  • 单元格中的值通常就是你要优化的值。
  • 每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。
  • 没有放之四海皆准的计算动态规划解决方案的公式。

K 最近邻算法

  • KNN用于分类和回归，需要考虑最近的邻居。
  • 分类就是编组。
  • 回归就是预测结果（如数字）。
  • 特征抽取意味着将物品（如水果或用户）转换为一系列可比较的数字。
  • 能否挑选合适的特征事关KNN算法的成败。

堆数据结构

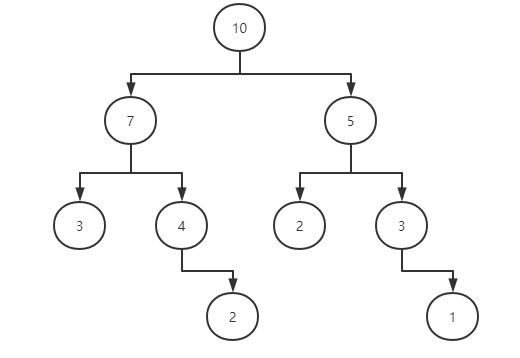
数据结构与二叉树的层序遍历类似，即按每层从左往右添加到数组。

最大堆：父节点值比所有子节点值都要大；

最小堆：父节点值比所有子节点值都要小；

堆1

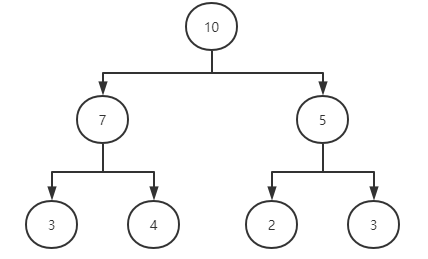
数组表示堆：[10, 7, 5, 3, 4, 2, 3]

堆2

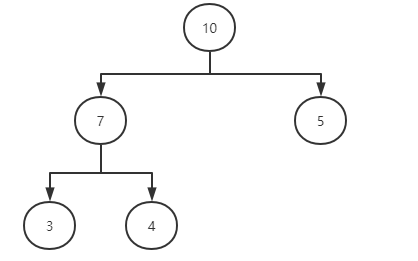
数组表示堆：[10, 7, 5, 3, 4]

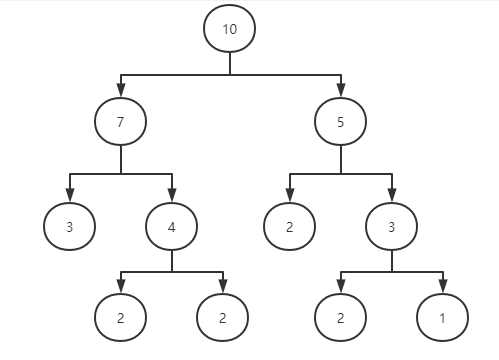
注意：创建堆数据结构是对二叉树的节点从左到右填值，不能跳过中间节点，否则不成立。

下面的堆数据结构不成立：

堆3堆4